Find the best formulation according to price, properties, similarity with a target composition, combining different raw materials. The platform assists in the formulation of products like ceramic bodies and their coatings (engobes, glazes, frits, additives, inks) thanks to its flexible mathematical optimization algorithms.

The archived properties and measurements can be used as boundaries or optimization targets while reformulating an existing product, to obtain the best cost, loss of ignition, absence of unwanted oxides or minerals - based on operator’s experience and previous studies. It is possible to define custom parameters through arbitrary formulae.

Multi-constrained optimization

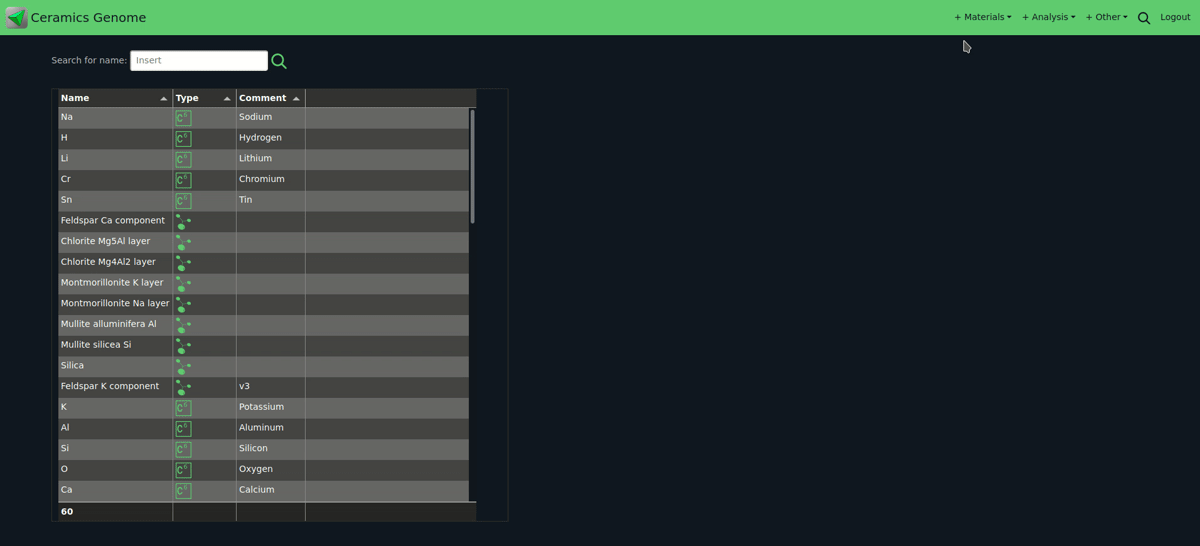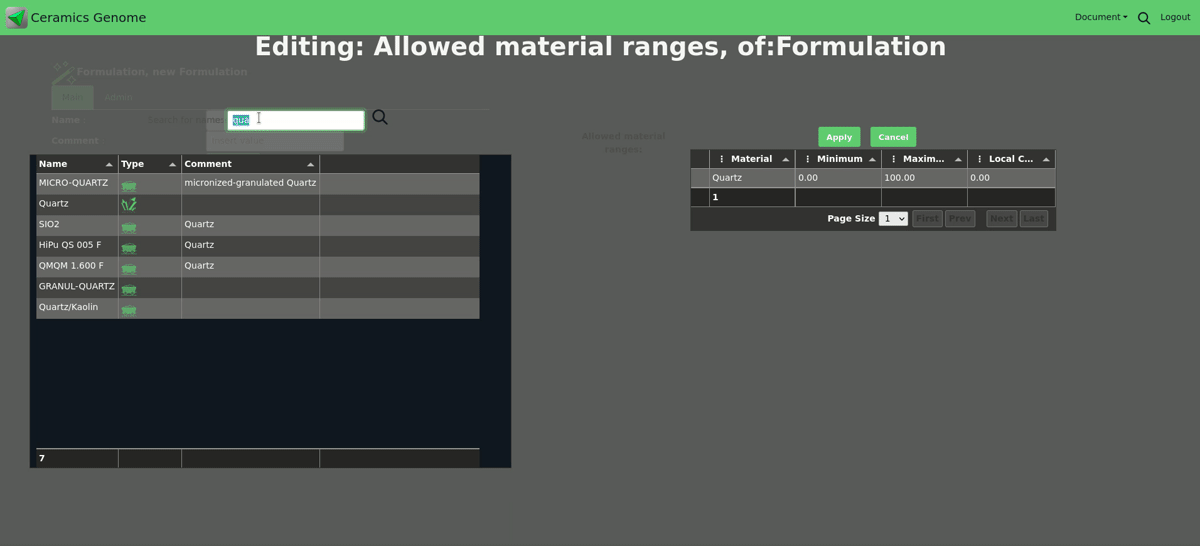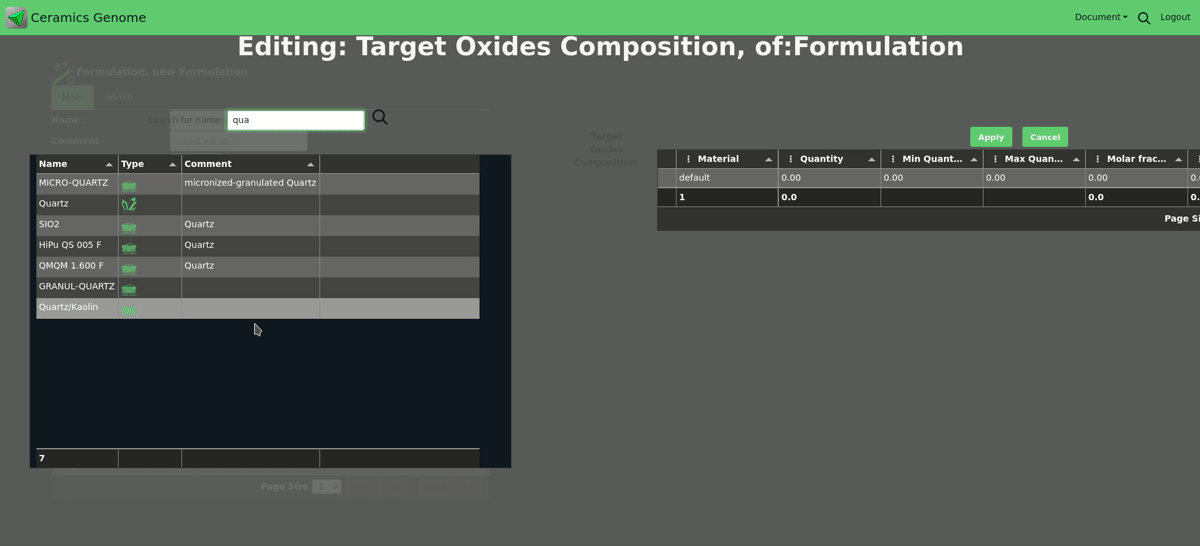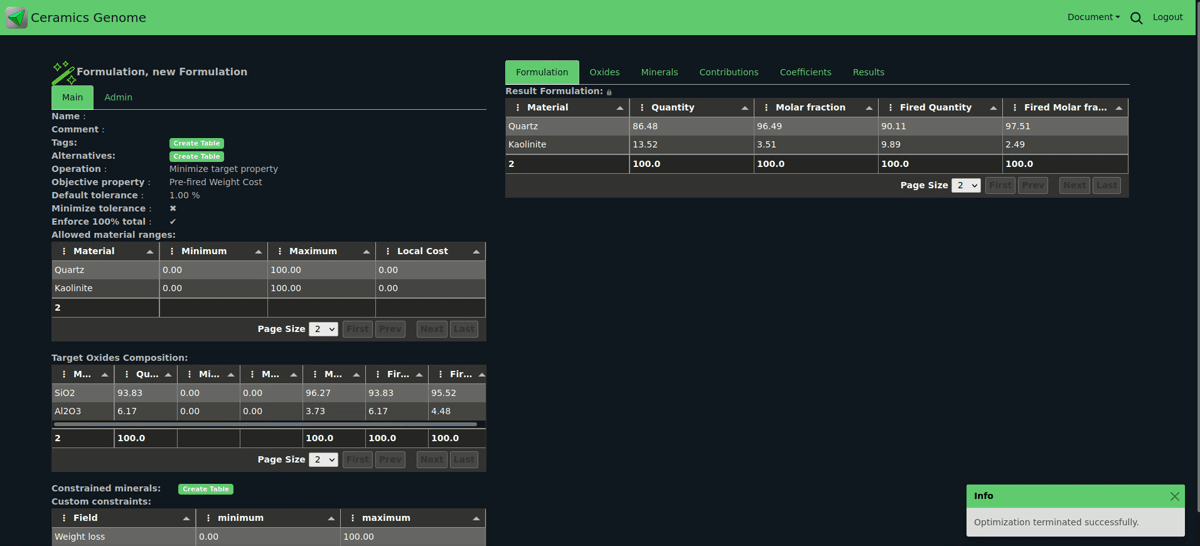
Given a pool of available materials, each having a target numerical property, the optimization algorithm can minimize (or maximize) the property of a mixture by finding the best proportions of the starting materials.

A typical target property is, for example, the unfired cost of the raw materials.

The target property alone is not enough to obtain interesting results: if cost if the target, the solution would trivially be 100% of the cheapest material in the pool of available components.

The optimization becomes insightful when proper constraints are applied. The most important are composition constraints:

• Require that the final composition in oxides or minerals is within a tolerance of a given target composition
• Require that the materials in the available pool are used within a certain range
• Require that a specific oxide or mineral is contained within a range

These constraints, applicable simultaneously, allow the reformulation of a product given different raw materials, while respecting the overall oxide or mineralogical composition.

Iterative composition tolerance minimization

If the algorithm cannot find any solution within the given tolerance from the target composition, it will simply fail. Ceramics Genome allows to find the minimum composition tolerance required in order to succeed, by iteratively minimizing an expressly large tolerance.

Customized cost functions

The standard materials' properties or attributes, as loss of ignition or cost, might not be able to express, by themselves, the preferences the ceramist would like to guide the algorithm.

The system allows to define customized new numerical properties by defining mathematical formulae that incorporate existing properties. This system can be used to define a complex cost function, that combines economical cost with many other parameters and weights them according to the user’s preference.

The new field will be used to guide the algorithm to the best solution, given an arbitrarily complex cost function.

Multi-variate recursive optimization

Ceramics Genome makes easy defining a custom cost function. Nonetheless, its conceptual design and the interpretation of its behaviour can be challenging.

A cost function will frequently combine incomparable quantities, like a cost, a loss of ignition, and maybe even an oxide or mineral content. Scaling and balancing those values in a meaningful cost function can be daunting.

Ceramics Genome introduces the recursive optimization, which will most of the time make superfluous the definition of a custom cost function.

Imagine you want to minimize cost and LOI, within a well-defined frame of the formerly exposed constraints. Through recursive optimization, it is possible to run two distinct optimization in series:

1. The first optimization will minimize cost alone, as usual. Suppose it finds a combination costing 100€/ton.
2. The second optimization will optimize LOI, while loosening the requirements on the cost by a given tolerance. For example, we search the minimum LOI composition having a cost between 90€ and 110€/ton.

This procedure can be extended to multiple parameters in series. Each step introduces new dynamical constraints, based on the result of the optimization and on a tolerance we provide at the beginning of the calculation.

In other words, the user must evaluate “how much of property A am I willing to sacrifice to also optimize property B?”. And then C, D, etc… for how many properties as needed.

This leads to the best solution, given the tolerances we define along the recursion path.